Schwarz–Ahlfors–Pick theorem
In mathematics, the Schwarz–Ahlfors–Pick theorem is an extension of the Schwarz lemma for hyperbolic geometry, such as the Poincaré half-plane model. It states that the Poincaré metric is distance-decreasing on harmonic functions.
The theorem states that every holomorphic function on the unit disk U, or the upper half-plane H, with distances defined by the Poincaré metric, is a contraction mapping. That is, every such analytic mapping will not increase the distance between points. Stated more precisely:
Theorem: (Schwarz–Ahlfors–Pick) For all holomorphic functions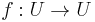 
, one has 
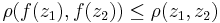for points 
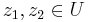and Poincaré distance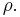 
For any tangent vector T, the hyperbolic length of the tangent vector does not increase:
